可以绘制用于电路分析的许多不同方程式。Take for instance Ohm’s Law for a 1 kΩ resistor:
|
|
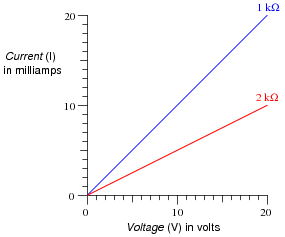
按照欧姆定律绘制此图。然后,绘制另一个表示2kΩ电阻的电压/电流关系的图。
|
|
一种sk your students to explain how they plotted the two functions. Did they make a table of values first? Did they draw dots on the paper and then connect those dots with a line? Did anyone plot dots for the endpoints and then draw a straight line in between because they knew this was a linear function?
可以绘制用于电路分析的许多不同方程式。以欧姆法律为例,以获取与12伏来源相关的可变电阻器:
|
|
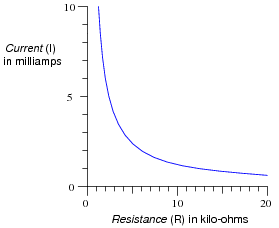
按照欧姆定律绘制此图。
|
|
一种sk your students to explain how they plotted the two functions. Did they make a table of values first? Did they draw dots on the paper and then connect those dots with a line? Did anyone plot dots for the endpoints and then draw a straight line in between because they knew this was a linear function?
Many students are surprised that the plot is nonlinear, being that resistors are considered linear devices!
Observe the following equivalence:
|
Since all operations are the same (multiplication) and reversible, the parentheses are not needed. Therefore, we may write the expression like this:
|
Of course, the simplest way to write this is 45, since there are five 4’s multiplied together.
扩展这些表达式中的每一个,因此也没有指数:
一种fter expanding each of these expressions, re-write each one in simplest form: one number to a power, just like the final form of the example given (45)。From these examples, what pattern do you see with exponents of products. In other words, what is the general solution to the following expression?
|
|
我发现无法理解一般规则的学生(一个m× an=一种m+n)通常是第一次看到具体的例子。
Observe the following equivalence:
|
It should be readily apparent that we may cancel out two quantities from both top and bottom of the fraction, so in the end we are left with this:
|
re-writing this using exponents, we get 41。
扩展这些表达式中的每一个,因此也没有指数:
\((\frac{3^5}{3^2})\) =
\((\frac{10^6}{10^4})\) =
\(((\ frac {8^7} {8^3})\)=
\((\ frac {20^5} {20^4})\)=
一种fter expanding each of these expressions, re-write each one in simplest form: one number to a power, just like the final form of the example given (41)。From these examples, what pattern do you see with exponents of products. In other words, what is the general solution to the following expression?
|
|
I have found that students who cannot fathom the general rule \((\frac{a^m}{a^n} = a^{m-n}) \) often understand for the first time when they see concrete examples.
Observe the following equivalence:
|
It should be readily apparent that we may cancel out two quantities from both top and bottom of the fraction, so in the end we are left with this:
|
佛llowing the rule of \((\frac{a^m}{a^n} = a^{m-n})\), the reduction of \((\frac{4^2}{4^3})\) should be 4-1。许多学生发现这令人困惑,因为指数的直观概念(本身要乘以多少次)在这里失败。在世界上,我们如何将4乘以-1次?!
扩展这些表达式中的每一个,因此也没有指数:
\((\frac{3^2}{3^5})\) =
\(((\ frac {10^4} {10^6})\)=
\(((\ frac {8^3} {8^7})\)=
\((\frac{20^4}{20^5})\) =
另外,扩展以下表达式,因此没有指数,然后按照规则\(((\ frac {a^m} {a^n} = a^a^{m-n})\)重写指数形式的结果。
|
What does this tell you about exponents of zero?
负指数仅仅是其正对应物的倒数(1/x)。零指数始终等于1。
我发现无法理解负面指数或零指数的含义的学生通常会立即理解自己的定义基于一般规则\(((\ frac {a^m} {a^m} {a^n} = A^a^{m-n})\)。
When evaluating (calculating) a mathematical expression, what order should you do the various expressions in? In other words, which comes first: multiplication, division, addition, subtraction, powers, roots, parentheses, etc.; and then what comes after that, and after that?
首先执行括号内的操作(如果有多个括号的层),功率和根,函数(Trig,Log等),乘法/除法,最后是加法/减法。
Order of operations is extremely important, as it becomes critical to recognize proper order of evaluation when “stripping” an expression down to isolate a particular variable. In essence, the normal order of operations is reversed when “undoing” an expression, so students must recognize what the proper order of operations is.
佛llow proper order of operations to evaluate these expressions:
$$ \ frac {13 + 2} {3} + 8 = $$
$$ 25 +(3 + 2)^2 x 2 = $$
$$\frac{13 + 2}{3} + 8 = 13$$
$$25 + (3+2)^2 x 2 = 75$$
Nothing special here - just simple arithmetic problems that cannot be solved correctly unless proper order of operations is followed.
佛llow proper order of operations to evaluate these expressions:
$$\frac{15 - 3}{3} + 7 = $$
$$20 + (1+3)^2 x 3 = $$
$$\frac{15 - 3}{3} + 7 = 11$$
$$ 20 +(1 + 3)^2 x 3 = 68 $$
Nothing special here - just simple arithmetic problems that cannot be solved correctly unless proper order of operations is followed.
在评估这样的表达式时,遵循适当的操作顺序非常重要。否则,正确的结果将无法得出:
|
To show what the proper order of operations is for this expression, I show it being evaluatedstep by stephere
|
|
|
|
|
对以下每个表达式执行相同的操作:
by the way, this is a highly recommended practice for those struggling with mathematical principles:记录每个步骤通过重写表达方式。尽管它需要更多的纸和更多的精力,但它会使您免于不必要的错误和挫败感
呢
我会让您确定并记录适当的操作顺序,但这是每个表达式的结果:
Order of operations is extremely important, as it becomes critical to recognize proper order of evaluation when ßtripping” an expression down to isolate a particular variable. In essence, the normal order of operations is reversed when ündoing” an expression, so students must recognize what the proper order of operations is.
Perform the following calculations:
|
|
Nothing special here, just practice with exponents.
Perform the following calculations:
|
|
Nothing special here, just practice with exponents.
The equation for calculating total resistance in a parallel circuit (for any number of parallel resistances) is sometimes written like this:
|
re-write this equation in such a way that it no longer contains any exponents.
|
This question is an exercise in basic algebra, specifically the meaning of negative exponents.
一种functionis a mathematical relationship with an input (usually x) and an output (usually y). Here is an example of a simple function:
|
显示任何给定功能的模式的一种方法是使用数字表。完成此表的给定值x的值:
|
||||||||||||||||||||||||||||||
显示任何给定功能的模式的一种更常见的(和直觉)的方法是图形。完成此图的相同函数y = 2x 1.考虑轴上的每个划分为1个单位:
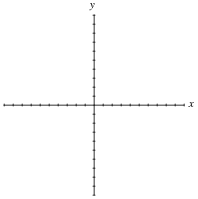
|
|
|
||||||||||||||||||||||||||||||
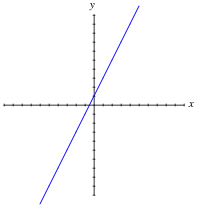
|
|
It is very important for your students to understand graphs, as they are very frequently used to illustrate the behavior of circuits and mathematical functions alike. Discuss with them how the line represents a continuous string of points and not just the integer values calculated in the table.
理解指数的著名说明性故事是这样的:
不过,在短时间内,国王发现自己破产了贫民,因为大米的数量非常大。这就是指数函数的性质:它们在x中的增长幅度非常大。
Graph the pauper’s rice function (y = 2X), with each division on the horizontal axis representing 1 unit and each division on the vertical axis representing 100 units.
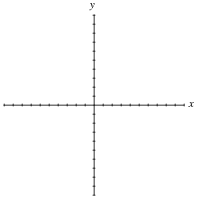
|
|
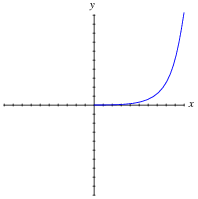
|
|
佛llow-up question: what do you think this graph will look like for negative values of x?
从显示的图表中,可能似乎随着x接近零的函数即将接近0。事实并非如此,因为简单的计算(y = 20)shows. In order for students to adequately see what is going on near the origin, they will have to re-scale the graph.
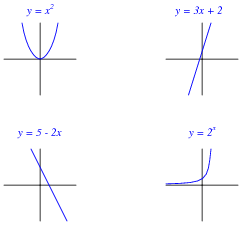
Match each written function (y = …) with the sketched graph it fits best:
|
|
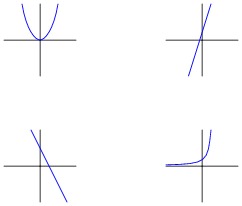
|
|
|
|
The primary purpose of this question is to have students figure out如何to match each expression to a graph. Of course, one could take the time to plot each function one by one, but there exist much simpler ways to determine the “character” of a function without plotting the whole thing.
Match each written function (y = …) with the sketched graph it fits best:
|
|

|
|
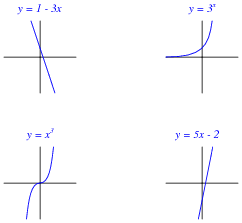
|
|
The primary purpose of this question is to have students figure out如何to match each expression to a graph. Of course, one could take the time to plot each function one by one, but there exist much simpler ways to determine the “character” of a function without plotting the whole thing.
Published under the terms and conditions of the创作共用一种ttribution License
问题3,答案 - “ = a^(m+n)”中缺少“+”符号。
Question 7, question and answer - second equation should have a multiplication symbol, not the ‘variable x’.
Question 8, question and answer - second equation should have a multiplication symbol, not the ‘variable x’.
Question 9, question - the ‘+’ symbol is missing between ‘4.5154 ‘+’ 14’.
问题9,答案:
-the ‘+’ symbol is missing: 10 − 25 ×2 ‘+’ 5 = −35
——“+”符号缺失:−8 ' + ' 10 ^ 3×51 = 50992
- 缺少“+”符号:12^4×(3'+’11)= 290304
Question 9, question and answer: The square root should enclose the whole equation, and the equation should have a multiplication symbol, not the ‘variable x’.
问题13,问题和答案:表列需要间距,而“ 2x + 1”标题中缺少“ +”符号。
These are all correct in the PDF version.